Color space in video (part 1)

Have you ever wondered how a color can be represented in a video and how it can be reproduced on a wide variety of screens with almost the same rendering? Part of the answer lies in the concept of color space.

This first article will discuss the color theory and define the key elements necessary to build a color space for digital videos. A second part will follow and will focus on the most commonly known color spaces in the video/TV domain and how to analyze them using ffmpeg. So, let’s jump into the theory and talk about our eye capacities!

A bit of biology

We cannot talk about colors without talking about our eye. As you will see, it is important to understand its capacities and weaknesses to efficiently represent colors in digital videos.

First, sorry to tell you that but colors do not exist in reality. Our eye can detect a subset of electromagnetic wavelengths from 380 to 700 nanometers; this is called the visible spectrum, and colors are an interpretation of our brain based on the wavelengths received by our eye. And it could act strangely. For example, the same exact color can be produced using different combination of wavelengths; this phenomenon is called metamerism. A simple example is the yellow color, it could be a single wavelength at 580 nanometers, but it can also be a mix of red and green wavelengths. Also almost all colors can be reproduced using a single wavelength except the magenta which is a mix of purple and red wavelengths.

To understand that behavior, we need to dig more into how our eye works. At its core, it is composed of rod cells and cone cells. rod cells can detect light brightness, they are mainly efficient in dark environments and are almost entirely responsible for our night vision. cone cells, on the other hand, can detect colors mainly in medium and high light brightness; they are of three types, S-cone, M-cone, and L-cone. Each cone cell has a specific response to wavelengths, and their peaks of sensitivity are respectively Blue (S-Cone), Green (M-cone), and Red (L-cone). They also have different sensitivity to brightness; concretely, the eye can detect more nuances of greens than it can for red ones or blue ones. To help you visualize how it works, here is a normalized view of the spectral sensitivity of each cone cell (keep in mind this is a normalized view, in fact, the peaks for each cone cell are not at the same level):

From there, we can explain the metamerism phenomena. The principle is to find different mix of wavelengths that produces the same response on S-cone, M-cone, and L-cone to get the same color. This is because cone cells generate an average response in the face of several wavelengths; therefore, you can get a yellow from a single wavelength but also by combining green and red, with an average response “in-between” on yellow. We can also explain why the magenta has no corresponding single wavelength. This is because it is a mix of extreme visible colors in the visible spectrum (purple and red), and no “in-between” single wavelength can produce the same response. Therefore our brain creates a new one to fill that gap.

That is a lot of concepts to digest, I know, but to oversimplify, what you can remember is that:

1. color is a brain interpretation of wavelengths received by our eye
2. our eye has a high sensitivity to brightness
3. our eye can detect colors with cone cells with a peak of sensitivity on Red, Green, and Blue
4. the same color could be produced using different combinations of wavelengths

Don’t worry; we will dig into the important concepts that are used to represent colors in the following sections.

How bright is it?

Each visible color is perceived by our eye with a different brightness and this not only depends on the light intensity (photons). Take these blue and green images:

You perceive the green one as brighter, don’t you? This is because our eye is more sensitive to the Green color than it is to Blue. Remember what we said about S-cone, M-cone, and L-cone? They don’t have the same sensitivity regarding brightness. That perceived brightness of a color is called luminance, and it depends on the light intensity, of course, but also on the color itself, as we have just seen.

The luminance is measured in candela per square meter, also called nits. To give you an idea of the scale, a typical scene at sunrise is ~25 nits. The sun's disk at noon is ~1.6 billion nits! But don’t look at it! You risk retinal damages at ~100 million nits 😎.

Are you dazzled?

Our eye can adapt to very wide luminance conditions. It can detect objects in very bright environments under sunlight but also in very dark environments during the night. The ratio between the highest luminance and lowest one can be as high as 15 000 000:1, but this is only achievable thanks to mechanical and chemical adaptions in our eye.

At a fixed configuration in a scene, our eye can distinguish luminance ratio from ~1 000:1 to ~15 000:1 depending on people and light conditions. When the ratio is higher, we start to lose information, and some colors disappear. This ratio between the highest and lowest luminance in a scene is called the dynamic range, and this is an important part to look at when trying to reproduce images that “feel“ more natural.

What can we perceive?

To define a model to represent colors, we need to know what colors are perceived by our eye.

The "Commission Internationale de l'éclairage" (CIE) studied human color vision and worked on a model to represent it. In 1931, they created the CIE XYZ color space to represent all visible colors. Hum, it is named a color space but keeps in mind this is not the same concept as the one used for digital videos. The Y component was deliberately designed to represent luminance. But for X and Z… it is a bit abstract. We need to understand how this space was built to understand them.

Before 1931, the CIE conducted several experiments with humans to match different source colors with a single wavelength using a combination of red, green, and blue lights. The aim was to leverage how cone cells work with the metamerism phenomena. But... it didn’t work for all colors. In fact, it was sometimes necessary to add some of the 3 red, green, and blue colors to the source light instead of mixing them to get a match. This resulted in the concept of negative colors 😯. Using these experiments, the CIE was able to define a Red, Green, and Blue color space (CIE RGB) where all visible colors were represented but using negative values, which was not very convenient:

To overcome this problem, the CIE worked on a mathematical transformation to get a color space only using positive values and luminance. We won’t enter the mathematical details here, but this resulted in the creation of the CIE XYZ color space. This is an abstract coordinate system but with the advantage of expressing any visible color with only positive values:

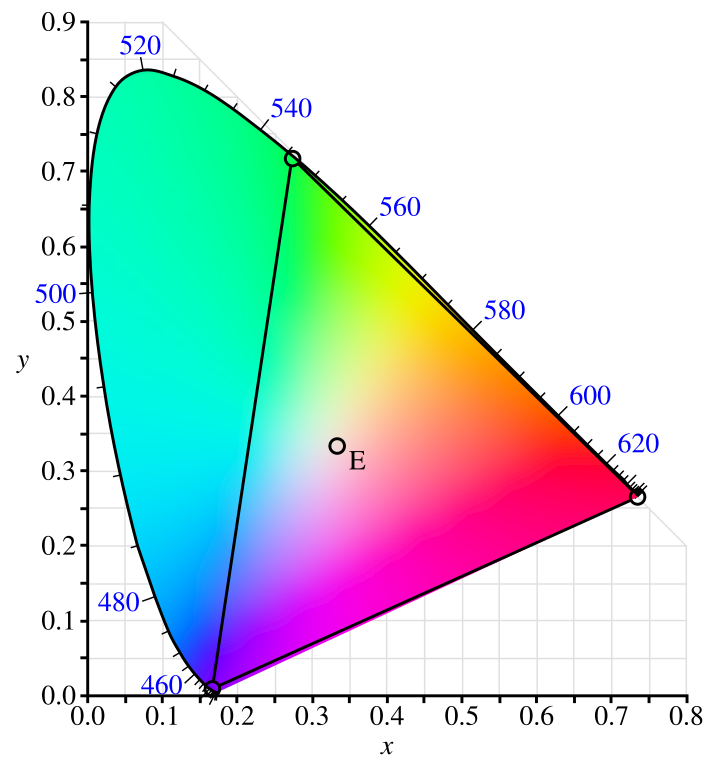
Well, you are lost? This is not over yet; another used system to represent visible colors is the CIE xyY. This is an equivalent color space to the CIE XYZ where (x, y) are normalized values independent from the luminance Y. There are called the chrominance. This color space is particularly useful as it allows to build a flat representation of colors at a given luminance which is called a chromaticity diagram:

Well, that diagram does not really represent all possible visible colors. First, you watch it through your screen, which cannot reproduce all colors. But more importantly, it is a flat view that could be built for each luminance value. A complete representation would require a 3 dimensions graph, but this one is more convenient for talking about color spaces, and we will use it in the second part for video color spaces.

Ok, just stop for a moment; there were a lot of things discussed, but what you should remember is:

1. the red, green, and blue lights cannot be used to reproduce all visible colors
2. the CIE built an abstract system to represent any visible color called CIE XYZ, where Y represents the luminance
3. the CIE xyY is an equivalent system to the CIE XYZ where (x, y) coordinates are independent of the luminance (Y) and are called chrominance
4. we have a convenient way to represent visible colors using the chromaticity diagram, even if it is not exhaustive  

How does this map to a video color space?

Now that we have the theory behind color, let’s deep dive into how to represent it for digital videos.

First, what colors do we target?

It is not practical in digital video to treat colors using all possible wavelengths. In the field, capturing devices rely on red, green, and blue cells to acquire color, and in the same way, screens re-produce them by combining red, green, and blue lights. Therefore a digital color is really tight to the RGB model, like in the CIE experiments. So, the first thing to define in a video color space is the reference red, green and blue colors to use in the CIE XYZ color space. These are called primary colors. All reachable colors in the video color space are contained within the triangle they formed in the chromaticity diagram. This also means that colors outside this triangle are not reproducible like we learned before! Here is the representation of the color space built by the CIE based on Red, Green, and Blue colors, e.g., CIE RGB. It is a really wide space, but as you can see, it does not cover all visible colors.

A color space also defines what is called the white point. Wait, what? Does that mean that we can choose what is white? Yes and no; when we talk about the white point we talk about a white object (in the common sense of white) observed using an ambient light. Depending on the ambient light, the object’s perceived color can vary. In digital video, the white point is often defined at a color temperature of 6500K. We won’t enter into the theory around why it is expressed using a temperature in Kelvin, but just remember that this value is, in fact, a white observed through the sun's daylight.

Do we really need them all?

Human eye sensitivity to contrast (luminance difference) is not linear. It is more sensitive to darker tones than it is to brighter ones. In digital videos, colors are represented using discrete values; consequently, it is impossible to represent them all. It would be a waste of data to encode things our eye is not good at distinguishing. To solve that, a color space defines a mathematical function to distribute colors more efficiently, knowing our eye capacities. This formula is called the transfer function. The luminance corrected by this transfer function is called the luma.

A pretty common transfer function you probably heard of if you played with your camera or TV settings is the gamma correction. This is a power-law expression for which the exponent (the power) is named gamma hence its name. A gamma of 1/2.2, represented here, emulates more or less the response of our eye to contrast:

As you see in the produced grayscale, thanks to the transfer function, we use more dark colors than bright ones with luma compared to the linear luminance distribution just below; this is exactly the purpose when using a transfer function.

Another part defined by a transfer function in video color space is the luminance range in nits at which it operates and, so indirectly, the reachable dynamic range. Remember what we said about the sun disk at noon? When you watch it in a video, hopefully, it does not burn your eye. This is precisely because of the chosen range; there is no need to be able to encode such a high luminance unless we want to injure people. And in any case, the screen you are using cannot reproduce it!

So all of this is great, but now, if we step back, the fundamental role achieved by a transfer function for digital video is compression! Indeed, if we have a really good way to choose colors that matter to our eye, it means we can use less of them without losing much visual quality.

Let’s focus on luminance

We discussed luminance and luma, but why does it matter? Can’t we use red, green, and blue instead? Well, we could, but it turns out this is not the most efficient way to represent colors in digital videos. Compression is really valuable in digital video; we already talked about the transfer function, but what if we can go deeper?

Again, we need to talk about our eye for that; if you remember, it is very good at distinguishing luminance but slightly less at distinguishing colors. To convince you about that, here is a simple optical illusion:

  Here triangles have the same color; can’t you see that? If you want to be convinced, click on the image.

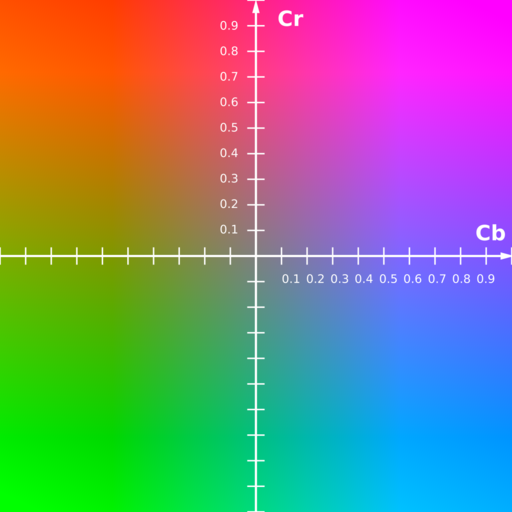
As disturbing as it is, we can use this to our advantage. For that, we need to represent a color by decomposing its pure luminance from its color contribution (chrominance). We already talked about such a thing in a previous section, and it is the CIE xyY. Indeed, a variation named Y'CbCr is used because it is more convenient for computers. Here Y' stands for the luma (luminance corrected by the transfer function), Cb for the blue contribution, and Cr for the red contribution. To help you visualize how it works, here is a plane distribution of colors at a fixed luma (Y’):

  If you look closely, this linear representation is, in fact, a stretched view of the primary colors triangle in the chromaticity diagram.

Now, with this system to represent a color, we can compress the color information even further. As we said, our eye is not good a distinguishing the chrominance compared to the luminance, so we can keep the luminance data for all pixels and use fewer chrominance values; why not take 1 out of 2 pixels? This is exactly what is done in digital video, and this process is known as chroma sub-sampling. Honestly, it is a bit more complex than just taking 1 pixel out of 2 for chrominance. A common compression is 4:2:0, meaning you take 4 pixels of luminance and 2 pixels of each chrominance on the first line, then 4 pixels of luminance and 0 pixels of each chrominance in the second line, resulting in an overall compression of 50%! It exists other compression schemes like 4:2:2, 4:1:1, 3:1:1… you get the idea it tells you how many chrominance pixels you take compared to luminance ones, and based on the scheme, you get a more or less compression ratio:

  Here is an image with different chroma sub-sampling schemes, it gives you an idea of the impact on the quality:

  Something is still missing here; how do we convert an R'G'B' color to Y'CbCr? There is no absolute formula to do this transformation, and that’s something a video color space must define.

Here is an example of the luma and chrominance calculation given its Red, Green, and Blue parts:

We can immediately see from this formula that the Green part contributes more to the luma than the Red and, finally, the Blue. Of course, this is because of our eye, if you remember what we said about our cone cells. All these coefficients (also for Cb and Cr) need to be defined by a video color space to ensure the conversion of a Y'CbCr color into its R'G'B' equivalent.

Now, a bit of history, you will often see YUV used interchangeably with YCbCr. In fact, YUV terms come from analog TVs, and YCbCr is its digital equivalent. As we have seen, the Y part is the luminance, but it is no more, no less than the black and white part of the color. It was used at first on black and white screens to convey images. When color TVs arrived, there was a choice to make whether to switch on a new color system like RGB or keep the black and white signal Y and add to it the color contribution or chrominance U and V. Of course; the second option was chosen to avoid a big breaking change between color and black and white TVs. This also explains why this color system is so widely used in video.

How many colors can we use?

Because colors are represented in a numeric format, we need to decide the number of bits that will be used to store them. Whether you use RGB or YCbCr you will need to encode three channels to encode a single color. The number of bits used to encode a single channel is called color depth. This number is directly linked to the range of colors it can represent. In the video domain, common values are:

• 8 bits: ~16 million colors
• 10 bits: ~1 billion colors
• 12 bits: ~69 billion colors

Remember that even if it seems huge, our eye can see much more colors than that.

So, you may wonder why don’t we use a bigger color depth ? This is because your video size would dramatically increase. Taking a single image in a 4K video requires encoding ~8 million colors, one for each pixel, representing ~285Mb using 12 bits color depth. And we only talk about a single image. Of course, they are ways to compress that, but this is just to give you an idea of how big it can be, even for a computer.

In that case, why don’t we use a smaller one? Like every time with computers, this is a trade-off. If we use a smaller color depth we may not be able to produce enough color shades. When looking at a gradient image, the transition between colors may not be smooth, and you will start to see some bands appearing. This effect is known as color banding, and of course, we want to avoid that. Here is an example of color banding on the left compared to a smooth color gradient on the right:

Don’t forget analog TVs

We cannot talk about digital videos without talking about analog ones. Due to technical constraints, the analog video signal was not only conveying information about colors; there was also non-visual data to sync new lines on the screen, for example. Also, due to its analog transport, colors were not always accurate. Because of that, when digital videos arrived, it was decided to reserve some values about the color data to encode non-visual information or conversion problems. This resulted in the creation of the color limited range or tv range.

Concretely, not all possible values were used to encode the color information. At that moment, colors were encoded using values from 0 to 255 (in 8 bits). It was decided to only use values from 16 to 235 for luma and 16 to 240 for chrominance. For the luma value, 16 is full black, and 235 is full white. That concretely means that we have fewer possible values to express colors. And this is always used for retro-compatibility in current digital videos, even for higher color depth. This is a specificity for videos and TV monitors; computers, on the other hand, use what is called a full range or pc range to express colors. It means all values from 0 to 255 are used to encode the color.

The color range information, either limited or full is therefore critical in a video color space to be able to reproduce colors accurately.

Conclusion

Great, you stayed focused until here! Here is a quick recap of what we have learned so far.

In order to build a color space for digital videos, we need to define:

1. Where are the primary colors and the white point to define what visible colors will be represented
2. What is the transfer function and its range in nits to use colors that matter to our eye in the best efficient way
3. What coefficients are used to convert YCbCr color into classic RGB and vice-versa?
4. What is the color depth used to know how many colors can be represented
5. Whether we use limited range (tv) or full range (pc) to encode color information

Is it all? Well, it would be too easy; a video color space also defines frame per second, resolution… and many other details. Here we only focus on generic concepts that define colors by abstracting video technical constraints.

If you want to learn more, stay tuned; in the next article, we will discuss standard video color spaces and how to identify them using ffmpeg.